Cartesiska kooordinater r = xˆx + yŷ + zẑ är de vanligaste men inte nödvändigtvis. Val av koordinatsystem beror på det problem vi vill studera.
|
|
|
- Gunnel Nyberg
- för 8 år sedan
- Visningar:
Transkript
1 yfte : 1 Fysikens matematiska metoder. Vecka 1 1. Vektoranalys. Definiera och analysera begrepp analysen för vektorfunktionen. 1.1 Varför vektorer : Rumskonceptet En punkt i ett normalt rum som lektionssalen kan uttryckas i form av koordinater. Vi beskriver punkten i form av (1) avståndet från väggen med tavlan, (2) Avståndet från fönsterväggen och (3) höjden över golvet. Dessa Cartesiska kooordinater r = xˆx + yŷ + zẑ är de vanligaste men inte nödvändigtvis de bästa alltid. Val av koordinatsystem beror på det problem vi vill studera. - En godtycklig rörelse i lektionssalen beskrivs bäst i Cartesiska koordinater. - Rörelsen hos en fluga som sitter på ett snurrande cykelhjul bör delas upp i en (1) cirkulär rörelse för ett system som består av flugan och hjulet och (2) en eventuell cartesisk beskrivning av flugans rörelse relativt det snurrande cykelhjulet. Cirkulärt polära koordinater beskriver bäst hjulets (1) rörelse { x = r cos θ y = r sin θ (1.1.1) - Rörelsen på en sfärs yta beskrivs gärna med sfäriskt polära koordinater. Varje enskild koordinat definierar i någon mening en riktning i rummet. I ett koordinatsystem kan basriktningarna vara vinkelräta i förhållande till varandra men de behöver inte vara det Vektorer i rummet. Fysiken behandlar händelser i rumtiden. - I Newtons mekanik är tiden helt oberoende av rummet. I Newtons mekanik är tiden en skalär. En punkt i det tredimensionella geometriska rummet kan karaktäriseras av avståndet från tre fixpunkter. Den kan också beskrivas som en vektor. En vektor har en längd eller en norm. r = xˆx + yŷ + zẑ (1.2.1) r = r = En vektor är uppbyggd av basvektorer eller komponeter och multiplikativa skalärer x, y och z. x 2 + y 2 + z 2 (1.2.2) ˆx, ŷ och ẑ (1.2.3)
2 2 Nils Elander, 08/ / :2:1 En enhetsvektor har normen ett ˆr = r r = xˆx + yŷ + zẑ r (1.2.4) Vektorer kan (1) adderas ( subtraheras ) och (2)multipliceras ( divideras ) med skalärer C = A + B = ˆx (x A + x B ) + ŷ (y A + y B ) + ẑ (z A + z B ) αa = α(xˆx + yŷ + zẑ) = (αx)ˆx + (αy)ŷ + (αz)ẑ Norm och skalärprodukt. addition skalärmultiplikation (1.2.5) Antag att två vektorer i rummet A och B har minst en basvektor ( ex. ˆx, ŷ eller ẑ ) gemensam. A = x Aˆx + y A ŷ + z A ẑ B = x Bˆx + y B ŷ + z B ẑ (1.2.6) Betrakta speciellt C = x C ˆx och A = x Aˆx + y A ŷ + z A ẑ (1.2.7) Uttrycket C A = (x C ˆx) (x Aˆx + y A ŷ + z A ẑ) = x C x A (ˆx) (ˆx) = x C x A (1.2.8) definierar skalärprodukten mellan C och A. - Då två vektorer alltid definierar ett plan kan man säga att skalärprodukten avbildar ett tvådimensionellt rum på en skalär. ( Denna skalär kan uppfattas som en yta) - Vi inser att skalärprodukten är kommutativ C A = A C (1.2.9) Relationen A ˆx = A x {ˆx ˆx} = A x (1.2.10) definierar projektionen av A på ˆx. Denna relation kan självfallet generaliseras till godtyckliga enhetsvektorer. Normen av en vektor definieras genom A A = A x A x (ˆx ˆx) + A y A y (ŷ ŷ) + A z A z (ẑ ẑ) + = A 2 x + A 2 y + A 2 z A = A 2 x + A 2 y + A 2 z (1.2.11)
3 3 Fysikens matematiska metoder. Vecka 1 Vektorprodukten. I tredimensionella rum finns ytterligare en relation mellan två vektorer vektorprodukten ˆx ŷ ẑ C = A B = A x A y A z (1.2.12) B x B y B z Vektorprodukten är anti-kommutativ. A B = B A (1.2.13) Man kan ur def. av skalärprodukt och vektorprodukt visa att A x A y A z A (B C) = B x B y B z C x C y C z med flera relationer. (1.2.14) 1.3. Polära och Axiella Vektorer samt Permutationssymboler för vektorräkning : Levi-Civita En vektor V som vid en koordinattransformation transformerar enligt ˆx i = a ijˆx j i = 1, 2, 3. (1.3.1) j=1 v i = a ij v j (1.3.2) j=1 där Ā = {a ij } är en ortogonalmatris kallas för en polär vektor eller rätt och slätt en vektor. En vektor W som vid en koordinattransformation transformerar enligt ˆx i = a ijˆx j i = 1, 2, 3. (1.3.3) j=1 w i = det(a ij ) a ij w j (1.3.4) j=1 kallas för en pseudovektor eller en axial vektor. Exempel : Kryssprodukten mellan två vektorer C = A B är en axial vektor. Detta inses ur att exempelvis C 1 = (A B) 1 = A 2 B 3 A 3 B 2 ej byter tecken då A s och B s komponenter byter tecken. Vinkelhastigheten ω för ett roterande hjul är en axial vektor ty den har sambandet v = ω r
4 4 Nils Elander, 08/ / :2:1 med ortsvektorn r från ett origo på axeln till en punkt på hjulet och en hastighet v för denna punkt. Både r och v är polär vektorer. Kryssproduktens nyss nämnda egenskap medför således att ω är en axial vektor. Tänk dessutom på hur det roterande hjulet ser ut i en spegel! Permutationssymbolen eller Levi-Civitas symbol har egenskapen +1 med (ijk) = (123), (312), (231) ɛ ijk = 1 med (ijk) = (132), (213), (321) 0 annars Vektorprodukten mellan två vektorer A och B (1.3.5) C i = j,k=1 ɛ ijk A j B k (1.3.6) ger en tredje (axial) vektor C = A B Betrakta kryssprodukten mellan bas vektorer (ˆx, ŷ, ẑ) = (ˆx 1, ˆx 2, ˆx 3 ) ˆx 1 = 1ˆx 1 + 0ˆx 2 + 0ˆx 3 ˆx 2 = 0ˆx 1 + 1ˆx 2 + 1ˆx 3 (1.3.6) ˆx 3 = 0ˆx 1 + 0ˆx 2 + 1ˆx 3 Vi får exemplvis att ˆx 1 ˆx 2 ˆx 3 ˆx 1 ˆx 1 = = ˆx 1 ( ) + ˆx 2 ( ) + ˆx 3 ( ) Eller Allmänt gäller att Detta innebär att ˆx 1 ˆx 1 = ɛ 121ˆx 1 + ɛ 122ˆx 2 + ɛ 123ˆx 3 ˆx i ˆx j = ɛ ijkˆx k. k=1 C = A B = ( m=1 A mˆx m ) ( n=1 B nˆx n ) = m,n=1 A m B n ( ˆx m ˆx n ) = A m B n ɛ mnj ˆx j m,n,j=1
5 5 Fysikens matematiska metoder. Vecka 1 Den j:te komponenten är alltså A B j = m,n=1 A m B n ɛ mnj Vid studier av problem med mer än en vektorprodukt ( skalärprodukt eller vektorprodukt ) vare sig produkten innehåller ren vektormultiplikation eller formallt derivator i form av olika typer av nablaoperatorer ( grad =, div =, eller rot = ) kan vi använda tre nyttiga relationer med Levi-Civita : ɛ mnk ɛ ijk = δ mi δ ni δ mj δ ni k (a) ɛ mjk ɛ njk = 2δ mn j,k (b) (1.3.7) ɛ 2 ijk = 6 j,k (c) Ekv.(1.3.7(c)) kan förstås genom att enbart permutationer av serien 123 ger bidrag och detta är (±1) 2. Det finns enbart sex sådana. Rimligheten av ekv.(1.3.6(b)) framgår om vi inser att varje term som har m n ger bidraget noll då den innehåller en upprepning av index. EXEMPEL : Låt m = 1, n = 2 och betrakta ekv.(1.3.7(b)) j = 1 ɛ 111 ɛ ɛ 112 ɛ ɛ 113 ɛ j = 2 ɛ 121 ɛ ɛ 122 ɛ ɛ 123 ɛ j = 3 ɛ 131 ɛ ɛ 132 ɛ ɛ 133 ɛ j,k ɛ 1jk ɛ 2jk = 2δ 12 = 0 Med m = 1 = n får vi däremot : j = 1 ɛ 111 ɛ ɛ 112 ɛ ɛ 113 ɛ j = 2 ɛ 121 ɛ ɛ 122 ɛ ɛ 123 ɛ j = 3 ɛ 131 ɛ ɛ 132 ɛ ɛ 133 ɛ j,k ɛ 1jk ɛ 1jk = 2δ 11 = 2
6 6 Nils Elander, 08/ / :2:1 För att förstå relationen (1.3.7(a)) bör man skriva upp ock kontrollera alla relationerna och det tar för mycket plats här. Relationer innehållande upprepade nablaoperatorer behabdlas med fördel med Levi-Civita. ekv.(1.5.6) är ett exempel på detta kalära fält och deras differentialer. Betrakta en funktion av flera variabler r = x, y, z,... vilken antar enbart ett värde för en given koordinat r φ = φ(x, y, z,...) = φ(r). (1.4.1) En sådan funktion kallas ett skalärt fält. Differentialen dφ(x, y, z,...) = φ x dx + φ y φ dy + dz +... (1.4.2) z kan skrivas dφ(x, y, z,...) = [ φ(x, y, z,...)] dr = ( φ (r) ) dr (1.4.3) där vi definierar φ(x, y, z,...) = φ(r) = ˆx φ x + ŷ φ y + ẑ φ z... dr = dx ˆx + dy ŷ + dz ẑ +... (1.4.4) Gradient eller nabla operatorn kan skrivas som φ (grad φ) ˆx φ x + ŷ φ y + ẑ φ +... (1.4.5) z Vektorn φ är normal ( vinkelrät ) till en yta definierad av φ = konstant och pekar i riktning av växande φ.
7 7 Fysikens matematiska metoder. Vecka 1 Laplaceoperatorn definieras genom φ = 2 φ φ = ˆx ˆx 2 φ x 2 + ŷ ŷ 2 φ y 2 + ẑ ẑ 2 φ z 2... = 2 φ x φ y φ z 2... (1.4.6) 1.5. Vektorfält och deras differentialer. Betrakta en funktional V = V(x, y, z,...) = V(r) vilken entydigt avbildar ett koordinatfält r = (ˆx x, ŷ y, ẑ z,...) (1.5.1) på ett vektorfält r = (x, y, z,...) V(x, y, z,...) = ˆx V x + ŷ V y + ẑ V z +... (1.5.2) Divergensen def. av V ( div V) = V x x + V y y + V z z +... (1.5.3) Rotationen def. för ett tredim. koord. system av ˆx ŷ ẑ V ( rot V) = x y z V x V y V z ( V3 = ˆx 1 V ) ( 2 V1 + ˆx 2 V ) ( 3 V2 + ˆx 3 V ) 1 x 2 x 3 x 3 x 1 x 1 x 2 (1.5.4) = mnl ɛ mnl ˆx m V l x n Laplaceoperatorn kan nu också definieras ur = 2 = = divgrad (1.5.5) Egenskaper beroende på att en determinant med två lika rader ( eller ) kolumner är identiskt lika med noll.
8 8 Nils Elander, 08/ / :2:1 - V är divergensfritt ( V) = i x i ( V) i = i x i j,k ɛ ijk V k = 0 (1.5.6) x j då ɛ ijk är antisymmetrisk. - vektorn φ är rotationsfritt ˆx ŷ ẑ ( φ) = x y z φ(r) = 0 (1.5.7) x y z 1.6. Linje och ytintegraler Linjeintegraler Betrakta en kurva C i rummet. Den har två ändpunkter 1 och 2. φ(r) dr vektor dr (1.6.1) C C C V(r) dr skalär (1.6.2) V(r) dr vektor dr och V (1.6.3) Betrakta ett infinitesimalt ytelement d. Ett riktat ytelement d = ˆn d (1.6.4) φ(r) d vektor (1.6.5) V(r) d skalär (1.6.6) V(r) d vektor (1.6.7)
9 9 Fysikens matematiska metoder. Vecka 1 1) Arbete : W Låt V vara ett kraftfält : V = F = φ W = F dr = C C dφ = [φ(1) φ(0)] (1.6.8) 2) Flöde : Φ. Låt V = v vara ett hastighetsfält. Φ = v(r) d = flödet genom ytan i riktningen ˆn (1.6.9) 1.7. Gauss sats, kontinuitetsekvationen och Greens sats Vad är divergens? Betrakta en liten volym dx dy dz ett hastighetsfält v(x, y, z) hos en komprimerbar vätska med tätheten ρ(x, y, z) i punkten (x, y, z). Flödet R in i denna volym genom sidan EF GH är R EF GH = ρv x x=0 dy dz (1.7.1)
10 10 Nils Elander, 08/ / :2:1 Flödet ut ur ( i positiv x led ) volymen genom sidan ABCD är R ABCD = ρv x x=dx dy dz (1.7.2) Nettoflödet erhålles genom expansion ( MacLaurin serie ) [ R ut ABCD = ρv x x=dx dy dz = ρv x + ] x (ρv x) dx x=0 dy dz (1.7.3) Derivata termen ger en första korrektion vilket tillåter oss att behandla en icke uniform täthet eller/och hastighet. Betraktar vi skillnaden får vi R netto ut i x = x (ρv x) dx dy dz (1.7.4) vilket ger oss gränsvärdet till en punktegenskap lim x 0 ρ v x ( x, 0, 0) ρ v x (0, 0, 0) x ρ v x(0, 0, 0) x (1.7.5) (0,0,0) Generellt i en godtycklig punkt (x, y, z) [ ρ vx R netto ut i (x,y,z) = x + ρ v y + ρ v ] z y z dx dy dz = (ρ v) dx dy dz (1.7.6) Nettoflödet hos en komprimerbar vätska ut ur ett volymselement dx dy dz per tidsenhet är (ρ v) därför kallas denna storhet divergensen En direkt tillämpning är Kontinuitetsekvationen : ρ t + (ρ v) = 0 (1.7.7) Kombinationen (fv) där f är en skalärfunktion och V är en vektorfunktion (fv) = x (fv x) + y (fv y) + z (fv z) = f x V x + f y V y + f z V z + f x V x + f y V y + f z V z (1.7.8) =( f) V + f( V) Gauss sats. Låt vara en volym omgiven av en sluten yta och låt ˆn vara normalen till en godtycklig punkt på ytan och låt dτ vara ett volymselement.
11 11 Fysikens matematiska metoder. Vecka 1 Gauss sats : V(r) dτ = V(r) d (1.7.9) Bevis Dela upp volymen i N infinitesimalt små volymer. En sådan volym går i gränsen N mot en punkt. Varje volym kan speciellt sönderdelas i små rektangulära volymer τ. För varje sådan liten rektangulär volym gäller enl. ekv.(1.7.6) ( Nettoflödet ) : R netto ut i (x,y,z) = (ρ v) dx dy dz sex sidoytor V d = V dτ (1.7.10) ummera över alla små lådvolymer kommer enbart de yttre sidorna att ge bidrag. Alla inre ytor kommer att räknas två gånger då riktningarna är motsatta. yttre ytor V d = V dτ (1.7.11) små volymer V d = V V dτ (1.7.9) Divergensen kan tolkas som nettoflödet per volymsenhet. Om V(r) 0 så finns det källor eller sänkor. Kontinuitetsekvationen på ett annat sätt. Betrakta en vätska i en volym som inte innehåller en källa eller en sänka. Volymen omges av en sluten yta. Då massan bevaras är det totala flödet ut genom in och ut genom beskrivet av t ρ(r)dτ = [ρ(r)v(r)] d = [ρ(r) v(r)] dτ (1.7.12) Då denna ekv. är oberoende av så gäller kontinuitetsekvationen : t ρ(r) + [(ρ(r)v(r)] = 0. (1.7.13) Gauss operatoridentitet och Greens identitet Betrakta ett vektorfält vilket kan sönderläggas i ett skalärfält och en konstant riktning V(r) = e i φ(r) e i = (x, y, z) med i = 1, 2, 3 (1.7.14) Applicera Gauss sats ( ekv.(1.7.9)) V(r) dτ = V(r) d d e i φ(r) = d i φ(r) = dτ e i φ(r) = dτ x i φ(r) (1.7.15)
12 12 Nils Elander, 08/ / :2:1 Då riktningen av koordinatenhetsvektorn e i är godtycklig gäller att d φ(r) = d i φ(r) = dτ φ(r) (1.7.16) i Om vi nu jämför Gauss sats V(r) dτ = V(r) d (1.7.9) med ekv. (1.7.16) får vi Gauss operator identitet d = dτ (1.7.17) Utnyttja (1.7.17) på A(r) till att ge d A(r) = dτ A(r) (1.7.18) Greens identitet kan härledas genom att man betraktar två skalära fält u(r) och v(r) och ur dem skapar vektorfältet u(r) v(r) v(r) u(r). Gauss operatoridentitet ( ekv.(1.7.17)) ger Greens identitet: d {u(r) v(r) v(r) u(r)} = = dτ [u(r) v(r) v(r) u(r)] dτ [ u(r) 2 v(r) v(r) 2 u(r) ] (1.7.19) 1.8. Rotation och tokes sats Cirkulationen Γ C av ett vektorfält V(r) definieras av Γ C (V x dx + V y dy + V z dz). (1.8.1) C Riktningen av cirkulationen är motsols och svarar mot skruvregeln ( se nedan). Vad är rotation? Betrakta integralen i (1.8.1) för att beskriva cirkulationen hos en vätska runt en liten ( infinitesimal ) slinga i xy planet. Γ C 1234 = V x (x, y) dλ x + V y (x, y) dλ y + V x (x, y) dλ x + V y (x, y) dλ y (1.8.2)
13 13 Fysikens matematiska metoder. Vecka 1 I de olika integralerna är dλ x = dx (1) dλ y = dy (2) dλ x = dx (3) (1.8.3) dλ y = dy (4) Integranderna är skrivna med avseende på en punkt (x 0, y 0 ) så att en Taylorexpansion kan användas. Exempel V y (x 0 + dx, y 0 ) = V y (x 0, y 0 ) + [ ] Vy x (x 0 y o ) dx +... (1.8.4) Detta ger : Γ C 1234 =V x (x 0, y 0 ) dx + [ V y (x 0, y 0 ) + V ] y x dx dy [ + V x (x 0, y 0 ) + V ] x y dy ( dx) + V y (x 0, y 0 )( dy) (1.8.5) = ( Vy x V ) x y Dividerar vi ekv.(1.8.5) med dx dy får vi dx dy Γ C 1234 /per enhetsyta = V
14 14 Nils Elander, 08/ / :2:1 tokes sats Låt vara en sluten yta och C dess rand. Betrakta ett vektorfält V(r) Låt oss nu betrakta rektangeln 1234 igen och dela upp den i små rektanglar. För en liten infinitisimal rektangel gäller V dλ = V d (1.8.6) de fyra sidorna ummera nu över alla små rektanglar. De inre linjeintegralerna tar ut varandra medan ytona adderas V dλ = V d (1.8.7) de yttre linjesegmenten små rektanglar C V dλ = V d (1.8.8) En operatoridentitet. Betrakta ett vektorfält i form av en given riktning och en skalär potential. Använd tokes sats V(r) dr = c V(r) = e i φ(r) d ( V(r) ) = Då detta gäller för alla i följer att dr φ(r) = i C e i C c φ(r) dx i = (d ) i φ(r) (1.8.9) dx i φ(r) = (d ) φ(r). (1.8.10) vilket generaliserar tokes teorem till en operatoridentitet dr = ( d ) (1.8.11) C
15 15 Fysikens matematiska metoder. Vecka Helmholz teorem Detta avsnitt klargör varför begreppen gradient, divergens och rotation är centrala i beskrivningen av vektorfält. Två teorem ges utan bevis. En entydighetssats En vektorfunktion i ett område är entydigt given av sin divergens och sin rotation inuti området och sin normalkomponent på områdets yta. Helmholz teorem Varje vektorfält V(r) kan uttryckas med hjälp av en skalär potential φ(r) och en vektorpotential A(r) V(r) = φ(r) + A(r) (1.9.1) - Den rotationsfria delen av fältet beskrivs av φ(r) - Den divergensfria delen av fältet beskrivs av A(r) V(r) = 2 φ(r) V(r) = ( A(r)) = ( A(r)) 2 A(r) Gauge kan väljas så att (1.9.2) ( A(r)) = 0 (1.9.3) kalär potentitialen φ(r) och vektorpotentialen A(r) är, som framgår av ekv.(1.9.2), lösningar till potentialekvationerna (Poissons ekvationer) : 2 φ(r) = s(r) 2 A(r) = (r) med s(r) = V(r) med (r) = V(r) (1.9.4) Här är s(r) den skalära källtätheten (vilken i elektrostatiken kallas laddningstätheten) och (r) är vektoriella källtätheten. Från elektrostatiken påminner vi oss att en skalär potential kan uttryckas som φ(r) = 1 s(r2 ) dτ 2 = 1 V(r2 ) dτ 2 r 12 = r 1 r 2 (1.9.5) 4π r 12 4π r 12 Medan motsvarande ekvation för vektorpotentialen ges av åledes A(r) = 1 (r2 ) dτ 2 = 1 V(r2 ) dτ 2 r 12 = r 1 r 2 (1.9.6) 4π r 12 4π r 12 - Divergensen av ett vektorfält kan tolkas som källtätheten för dess skalära potential.
16 16 Nils Elander, 08/ / :2:1 - Rotationen av ett vektorfält kan tolkas som källtätheten för dess vektoriella potential Ortogonala kroklinjära koordinatsystem. Hittills har vi antagit att de koordinatsystem vi arbetat med är Cartesiska. Vi vet emellertid att exempelvis sfäriskt polära koordinater är lämpliga att använda inom delar av atomfysiken. Generaliserade koordinater. Låt u 1, u 2, u 3 utgöra ett koordinatsystem vilket unikt kan uttrycka positionen i en 3-D rymd. Detta nya koordinatsystems relation till det Cartesiska systemet ges formellt av u i = u i (x, y, z) x i = x i (u 1, u 2, u 3 ) i = 1, 2, 3 (1.10.1) Exempel : färiskt polära koordinater r = (x 2 + y 2 + z 2 ) 1/2 θ = arctan[(x 2 + y 2 )/z 2 ] 1/2 φ = arctan(y/x) x = r sin θ cos φ y = r sin θ sin φ z = r cos θ Differentialer med vilket tillsammans ger dr = r u 1 du 1 + r u 2 du 2 + r u 3 du 3 (1.10.2) r = x ˆx + y ŷ + z ẑ = h i (r)û i (r) (1.10.3) u i u i u i u i dr = h i (r)û i (r)du i (1.10.4) i - Infinitesimala avstånd ds 2 = dr dr = h i (r)h j (r)du i du j = i,j g ij (r)du i du j (1.10.5) i,j torheten g ij (r) kallas en metrisk koefficient. ( Denna storhet är en andra ordningens tensor). Om vi sätter in (1.10.3) i (1.10.2) får vi g ij = x u i x u j + y u i y u j + z u i z u j (1.10.6) För ortogonala koordinater kan man visa att g ij = g ii δ ij. Ortogonala kroklinjära koordinater För ortogonala kroklinjära koordinater gäller speciellt û i û j = δ ij
17 17 Fysikens matematiska metoder. Vecka 1 vilket medför att ekv.(1.10.5) förenklas till ds 2 = h i (r)h i (r)(du i ) 2 = i g ii (r)(du i ) 2 = i (ds i ) 2 (1.10.7) i Exempel : - Cylindriska koordinater (ρ, φ, z) h ρ = 1, h φ = ρ, h z = 1 - färsikt polära koordinater(r, θ, φ) h r = 1, h θ = r, h φ = r sin θ Integraler. V dr = i V i h i du i (1.10.8) Om vi ur ds 2 = i (h i du i ) 2 (1.10.9) definierar ds i = h i du i ( ) kan vi bestämma yt- och volymselement som d ij = ds i ds j = h i h j du i du j och dτ = ds 1 ds 2 ds 3 = h 1 h 2 h 3 du 1 du 2 du 3 ( ) En ytintegralen kan då uttryckas som V d = V 1 h 2 h 3 du 2 du 3 + V 2 h 3 h 1 du 3 du 1 + V 3 h 1 h 2 du 1 du 2 ( ) Differentialrelationer i kroklinjära koordinatsystem. Gradient: Betrakta den komponent av φ(u 1, u 2, u 3 ) som är normal till den familj av ytor för vilka u 1 = konstant. φ = φ = φ (1.11.1) 1 s 1 h 1 u 1 Upprepar vi operationen i (1.11.1) för de övriga två generaliserade koordinaterna får vi Eller φ(u 1, u 2, u 3 ) = û 1 φ s 1 + û 2 φ s 2 + û 3 φ s 3 φ φ φ = û 1 + û 2 + û 3 h 1 u 1 h 2 u 2 h 3 u 3 φ = i=1 1 h i φ u i û i (1.11.2)
18 18 Nils Elander, 08/ / :2:1 Divergens: Betrakta Gauss sats Låt nu volymen gå i gräns och bilda V(r) dτ = V(r) d (1.7.9) V(u) = lim dτ 0 V d dτ (1.11.3) med dτ = ds 1 ds 2 ds 3 = h 1 h 2 h 3 du 1 du 2 du 3 Lägg märke till att u i bildar ett högerhandsystem så att û 1 û 2 = û 3 Ytintegralen för de två sidorna som svarar mot att u 1 = konstant ges på samma sätt som tidigare i avsnitt 1.7 av [ V 1 h 2 h 3 + ] (V 1 h 2 h 3 ) du 1 du 2 du 3 V 1 h 2 h 3 du 2 du 3 = u 1 Om vi generaliserar detta till alla riktningar får vi V = 1 h 1 h 2 h 3 [ u 1 (V 1 h 2 h 3 ) + u 2 (V 2 h 3 h 1 ) + u 1 (V 1 h 2 h 3 ) du 1 du 2 du 3 ] (V 3 h 1 h 2 ) u 3 (1.11.4) (1.11.5) Vi alltså visat Rotation: V = i=1 1 1 (p i V i ) med p i = h 1h 2 h 3 p i h i u i h i
19 19 Fysikens matematiska metoder. Vecka 1 Betrakta på samma sätt som för divergensen en yta med konstant u 1 Ur V d = V h 2 h 3 du 2 du 3 (1.11.6) 1 och genom att utnyttja tokes sats V dλ = V d (1.8.8) får vi att V h 2 h 3 du 2 du 3 = 1 V dλ (1.11.7) då linjeintegralen i ytan som definieras av att u 1 = konstant. Genom att följa slingan i figuren får vi V dλ = V 2 h 2 du 2 + [ V 3 h 3 + ] (V 3 h 3 ) du 2 u 2 du 3 [ V 2 h 2 + ] (V 2 h 2 ) du 3 u 3 du 2 V 3 h 3 = [ (h 3 V 3 ) ] (h 2 V 2 ) u 2 u 3 du 2 du 3 (1.11.8) Låt nu ytan gå i gräns du i 0 V = 1 1 h 2 h 3 [ u 2 (h 3 V 3 ) ] (h 2 V 2 ) u 3 (1.11.9)
20 20 Nils Elander, 08/ / :2:1 Generalisera till alla tre dimensionerna 1 V = h 1 h 2 h 3 h 1 û 1 h 2 û 2 h 3 û 3 u 1 u 2 u 3 h 1 V 1 h 2 V 2 h 3 V 3 ( )
Vektoranalys I. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
Vektoranalys I Anders Karlsson Institutionen för elektro- och informationsteknik 2 september 2015 Översikt över de tre föreläsningarna 1. Grundläggande begrepp inom vektoranalysen, nablaoperatorn samt
Integraler av vektorfält Mats Persson
 Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
Föreläsning 1/8 Integraler av vektorfält Mats Persson 1 Linjeintegraler Exempel: En partikel rör sig längs en kurva r(τ) under inverkan av en kraft F(r). i vill då beräkna arbetet som kraften utövar på
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 4, 2018 1. Fält och derivator Ett fält är en fysikalisk storhet
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 4, 2018 1. Fält och derivator Ett fält är en fysikalisk storhet
Föreläsning 2 1. Till varje punkt i rummet tilldelas en vektor. ( ) = T ( x, y, z,t) ( ) = v x
 Föreläsning 2 1 Matematiska grundbegrepp Fält kalärfält: Vektorfält: Till varje punkt i rummet tilldelas en skalär Exempel: Temperaturen i olika punkter i rummet, T r,t ( ) = T ( x, y, z,t) Till varje
Föreläsning 2 1 Matematiska grundbegrepp Fält kalärfält: Vektorfält: Till varje punkt i rummet tilldelas en skalär Exempel: Temperaturen i olika punkter i rummet, T r,t ( ) = T ( x, y, z,t) Till varje
Kroklinjiga koordinater och räkning med vektoroperatorer. Henrik Johanneson/(Mats Persson)
 Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
Föreläsning 7/9 Kroklinjiga koordinater räkning med vektoroperatorer Kroklinjiga koordinater Henrik Johanneson/Mats Persson) Allmänt behöver vi tre parametrar u, u 2, u 3 för att beskriva en godtycklig
1 Några elementära operationer.
 Föreläsning Några elementära operationer. Ett skalärfält är en reellvärd eller komplexvärd funktion Φ(x, y, z). Ett vektorfält är en vektorvärd funktion A(x, y, z). I ett kartesiskt koordinatsystem kan
Föreläsning Några elementära operationer. Ett skalärfält är en reellvärd eller komplexvärd funktion Φ(x, y, z). Ett vektorfält är en vektorvärd funktion A(x, y, z). I ett kartesiskt koordinatsystem kan
1 Vektorer och tensorer
 Föreläsning 1. 1 Vektorer och tensorer Vi kommer att använda två olika beteckningar för vektorer. Enligt det första systemet använder vi fet stil för en vektor i typsatt text och ett vektorstreck då vi
Föreläsning 1. 1 Vektorer och tensorer Vi kommer att använda två olika beteckningar för vektorer. Enligt det första systemet använder vi fet stil för en vektor i typsatt text och ett vektorstreck då vi
VEKTORANALYS Kursprogram VT 2018
 VEKTORANALYS Kursprogram VT 2018 Allmänt om kursen Målsättningen med kursen är att lära ut ett antal grundläggande matematiska metoder, som under de fortsatta studierna kommer att tillämpas i flera olika
VEKTORANALYS Kursprogram VT 2018 Allmänt om kursen Målsättningen med kursen är att lära ut ett antal grundläggande matematiska metoder, som under de fortsatta studierna kommer att tillämpas i flera olika
FFM232, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM232, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 3, 2016 8. Potentialteori Konservativa fält och potentialer
FFM232, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Oct 3, 2016 8. Potentialteori Konservativa fält och potentialer
TATA44 Lösningar 26/10/2012.
 TATA44 Lösningar 6/1/1. 1. Lösning 1: Konen z x + y skär sfären x + y + (z 5 5 då 4z + (z 5 5 och enkla räkningar ger nu z z some ger z(z och vi ser att z eller z. Observera att punkter på sfären med z
TATA44 Lösningar 6/1/1. 1. Lösning 1: Konen z x + y skär sfären x + y + (z 5 5 då 4z + (z 5 5 och enkla räkningar ger nu z z some ger z(z och vi ser att z eller z. Observera att punkter på sfären med z
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar hristian Forssén, Institutionen för fysik, halmers, Göteborg, verige ep 6, 217 3. Integraler Det mesta av detta material förutsätts vara
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar hristian Forssén, Institutionen för fysik, halmers, Göteborg, verige ep 6, 217 3. Integraler Det mesta av detta material förutsätts vara
Föreläsning 16, SF1626 Flervariabelanalys
 Föreläsning 16, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 5 december 2017 KTH Rekommenderade uppgifter: 16.1: 3, 7, 11. 16.2: 9, 15, 17. Gradient, divergens, och rotation Gradienten Om
Föreläsning 16, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 5 december 2017 KTH Rekommenderade uppgifter: 16.1: 3, 7, 11. 16.2: 9, 15, 17. Gradient, divergens, och rotation Gradienten Om
TATA44 ösningar till tentamen 13/01/ ) Paraboloiden z = 2 x 2 y 2 skär konen z = x 2 + y 2 då x 2 + y 2 = 2 x 2 y 2. Med
 TATA44 ösningar till tentamen 1/1/211. 1. Paraboloiden z 2 x 2 y 2 skär konen z x 2 + y 2 då x 2 + y 2 2 x 2 y 2. Med ρ x 2 + y 2 då är ρ 2 + ρ 2 vilket ger ρ + 2ρ 1. åledes är ρ 1 ty ρ. Vi betecknar den
TATA44 ösningar till tentamen 1/1/211. 1. Paraboloiden z 2 x 2 y 2 skär konen z x 2 + y 2 då x 2 + y 2 2 x 2 y 2. Med ρ x 2 + y 2 då är ρ 2 + ρ 2 vilket ger ρ + 2ρ 1. åledes är ρ 1 ty ρ. Vi betecknar den
1.1 Gradienten i kroklinjiga koordinatsystem
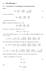 1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
1 Föreläsning 4 1.1 Gradienten i kroklinjiga koordinatsystem Sats 1 i sfäriska koordinater; i cylindriska koordinater. Bevis. I kartesiska koordinater har vi att Φ = r ˆr + 1 r θ ˆθ + 1 ˆϕ (1 r sin θ ϕ
1.1 Stokes sats. Bevis. Ramgard, s.70
 1 Föreläsning 7 1.1 tokes sats ats 1 åt vara en yta i R med randen. Vi antar att orienteringen på och är vald på ett sådant sätt att om man går längs i den valda riktningen då ligger till vänster (på vänstersidan).
1 Föreläsning 7 1.1 tokes sats ats 1 åt vara en yta i R med randen. Vi antar att orienteringen på och är vald på ett sådant sätt att om man går längs i den valda riktningen då ligger till vänster (på vänstersidan).
1 Allmänt om vektorer och vektorvärda funktioner
 1 llmänt om vektorer och vektorvärda funktioner 1.1 Vektorer och skalärer Inom fysiken gör vi skillnad på skalära och vektoriella storheter. Det som kännetecknar skalära storheter är att de har både storlek
1 llmänt om vektorer och vektorvärda funktioner 1.1 Vektorer och skalärer Inom fysiken gör vi skillnad på skalära och vektoriella storheter. Det som kännetecknar skalära storheter är att de har både storlek
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232)
 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232) Tid och plats: Lösningsskiss: Tisdagen den 20 december 2016 klockan 0830-1230 i M-huset Christian Forssén Detta är enbart en skiss av den
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM232) Tid och plats: Lösningsskiss: Tisdagen den 20 december 2016 klockan 0830-1230 i M-huset Christian Forssén Detta är enbart en skiss av den
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 11, 2017 12. Tensorer Introduktion till tensorbegreppet Fysikaliska
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 11, 2017 12. Tensorer Introduktion till tensorbegreppet Fysikaliska
Allmant behover vi tre parametrar u 1 u 2 u 3 for att beskriva engodtycklig punkt i rummet. Vi kan
 Forelasning 3/9 Kroklinjiga koordinater rakning med vektoroperatorer Kroklinjiga koordinater Allmant behover vi tre parametrar u u 2 u 3 for att beskriva engodtycklig punkt i rummet. Vi kan da skriva ortsvektorn
Forelasning 3/9 Kroklinjiga koordinater rakning med vektoroperatorer Kroklinjiga koordinater Allmant behover vi tre parametrar u u 2 u 3 for att beskriva engodtycklig punkt i rummet. Vi kan da skriva ortsvektorn
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
SF626 Flervariabelanalys Lösningsförslag till tentamen 23-5-27 DEL A. Bestäm alla punkter på ytan z = x 2 + 4y 2 i vilka tangentplanet är parallellt med planet x + y + z =. 4 p) Lösning. Tangentplanet
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 14, 2018 5. Indexnotation Precis som vi har räkneregler för
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 14, 2018 5. Indexnotation Precis som vi har räkneregler för
0. Introduktion, matematisk bakgrund
 0. Introduktion, matematisk bakgrund Kai Nordlund vt. 2013. Dessa anteckningar baserar sig i mycket stor utsträckning på anteckningarna förberedda av FD Krister Henriksson till kursen ht. 2005. Vissa delar,
0. Introduktion, matematisk bakgrund Kai Nordlund vt. 2013. Dessa anteckningar baserar sig i mycket stor utsträckning på anteckningarna förberedda av FD Krister Henriksson till kursen ht. 2005. Vissa delar,
SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december Lösningsförslag. F n ds,
 Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
Institutionen för matematik, KTH Serguei Shimorin SF1649, Vektoranalys och komplexa funktioner Tentamen, måndagen den 19 december 211. Lösningsförslag 1. Räkna ut flödesintegral F n ds, där F = (x e y,
Vektoranalys II. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys II Anders Karlsson Institutionen för elektro- och informationsteknik 9 september 215 Översikt 1 Kurvor och ytor, linje- och yt-mått 2 Integraler, Kap. 1.3 Linjeintegraler Ytintegraler Volymsintegraler
Vektoranalys II Anders Karlsson Institutionen för elektro- och informationsteknik 9 september 215 Översikt 1 Kurvor och ytor, linje- och yt-mått 2 Integraler, Kap. 1.3 Linjeintegraler Ytintegraler Volymsintegraler
SF1626 Flervariabelanalys Tentamen Torsdagen den 20 augusti 2015
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Torsdagen den 2 augusti 215 Skrivtid: 8:-1: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Torsdagen den 2 augusti 215 Skrivtid: 8:-1: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF166 Flervariabelanalys Lösningsförslag till tentamen 15-8- EL A 1. Betrakta funktionen f som är definierad i området där x + y genom f(x, y, z) x z x + y. (a) Beräkna gradienten f(x, y, z). (1 p) (b)
SF166 Flervariabelanalys Lösningsförslag till tentamen 15-8- EL A 1. Betrakta funktionen f som är definierad i området där x + y genom f(x, y, z) x z x + y. (a) Beräkna gradienten f(x, y, z). (1 p) (b)
TENTAMEN I VEKTORANALYS SI1146 och SI1140 Del 1, VT18
 TENTAMEN I EKTORANALY I46 och I40 Del, T8 Torsdagen 3 maj 4:00-9:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa ej
TENTAMEN I EKTORANALY I46 och I40 Del, T8 Torsdagen 3 maj 4:00-9:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa ej
Hydrodynamik Mats Persson
 Föreläsning 5/10 Hydrodynamik Mats Persson 1 De hydrodynamiska ekvationerna För att beskriva ett enkelt hydrodynamiskt flöde behöver man känna fluidens densitet,, tryck p hastighet u. I princip behöver
Föreläsning 5/10 Hydrodynamik Mats Persson 1 De hydrodynamiska ekvationerna För att beskriva ett enkelt hydrodynamiskt flöde behöver man känna fluidens densitet,, tryck p hastighet u. I princip behöver
OMTENTAMEN I VEKTORANALYS SI1146 och SI1140 Del 1, VT18
 OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
OMTENTAMEN I VEKTORANALY I46 och I40 Del, VT8 Onsdagen augusti 08:00-:00 Anteckna på varje blad: Namn, utbildningslinje, årskurs och problemnummer. Tillåtna hjälpmedel: Formelblad som delas ut. Räknedosa
Föreläsning 13, SF1626 Flervariabelanalys
 Föreläsning 13, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 28 november 2017 KTH Rekommenderade uppgifter: 15.1: 3, 5, 17. 15.2: 3, 5, 7, 21. Vektorfält DEFINITION Ett skalärfält Φ på ett
Föreläsning 13, SF1626 Flervariabelanalys Haakan Hedenmalm (KTH, Stockholm) 28 november 2017 KTH Rekommenderade uppgifter: 15.1: 3, 5, 17. 15.2: 3, 5, 7, 21. Vektorfält DEFINITION Ett skalärfält Φ på ett
1. Beräkna hastigheten, farten och accelerationen vid tiden t för en partikel vars rörelse beskrivs av r(t) = (2 sin t + cos t, 2 cos t sin t, 2t).
 Repetition, analys.. Beräkna hastigheten, farten och accelerationen vid tiden t för en partikel vars rörelse beskrivs av r(t) = (2 sin t + cos t, 2 cos t sin t, 2t). 2. Beräkna längden av kurvan r(t) =
Repetition, analys.. Beräkna hastigheten, farten och accelerationen vid tiden t för en partikel vars rörelse beskrivs av r(t) = (2 sin t + cos t, 2 cos t sin t, 2t). 2. Beräkna längden av kurvan r(t) =
Integraler av vektorfalt. Exempel: En partikel ror sig langs en kurva r( ) under inverkan av en kraft F(r). Vi vill
 Forelasning 6/9 ntegraler av vektorfalt Linjeintegraler Exempel: En partikel ror sig langs en kurva r( ) under inverkan av en kraft F(r). i vill da berakna arbetet som kraften utovar pa partikeln. Mellan
Forelasning 6/9 ntegraler av vektorfalt Linjeintegraler Exempel: En partikel ror sig langs en kurva r( ) under inverkan av en kraft F(r). i vill da berakna arbetet som kraften utovar pa partikeln. Mellan
Appendix A: Differentialoperatorer i olika koordinatsystem
 Appendix A: Differentialoperatorer i olika koordinatsystem [Arfken,BETA,Lahtinen] A. 1. Kurvilineära koordinatsystem Antag att i ett Cartesiskt (x, y, z) koordinatsystem med basvektorerna bx, by, bz existerar
Appendix A: Differentialoperatorer i olika koordinatsystem [Arfken,BETA,Lahtinen] A. 1. Kurvilineära koordinatsystem Antag att i ett Cartesiskt (x, y, z) koordinatsystem med basvektorerna bx, by, bz existerar
Tentamen SF1626, Analys i flera variabler, Svar och lösningsförslag. 2. en punkt på randkurvan förutom hörnen, eller
 Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
Tentamen SF66, Analys i flera variabler, --8 Svar och lösningsförslag. Låt fx, y) = ye x y. Bestäm största och minsta värde till f på den slutna kvadraten med hörn i, ),, ),, ) och, ). Lösning. f är kontinuerlig
Vektoranalys III. Anders Karlsson. Institutionen för elektro- och informationsteknik
 Vektoranalys III Anders Karlsson Institutionen för elektro- och informationsteknik 16 september 215 Översikt 1 Gauss sats divergenssatsen Exempel på användning av Gauss sats 2 tokes sats Exempel på användning
Vektoranalys III Anders Karlsson Institutionen för elektro- och informationsteknik 16 september 215 Översikt 1 Gauss sats divergenssatsen Exempel på användning av Gauss sats 2 tokes sats Exempel på användning
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
SF1626 Flervariabelanalys Lösningsförslag till tentamen 213-8-22 DEL A 1. Betrakta funktionen f(x, y) ln(x 2 + xy 2 4). a) Bestäm tangentplanet till funktionsytan z f(x, y) i den punkt på ytan där x 1
Institutionen för matematik SF1626 Flervariabelanalys. Lösningsförslag till tentamen Måndagen den 5 juni 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Måndagen den 5 juni 7 DEL A. En kulles höjd ges av z 6,x,y där enheten är meter på alla tre koordinataxlar. (a) I vilken
= 0. Båda skärningsvinklarna är således π/2 (ortogonala riktningsvektorer).
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
Institutionen för Matematik, KTH Torbjörn Kolsrud SF163, ifferential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen torsdag 19 augusti 21, 14. - 19. Inga hjälpmedel är tillåtna. Svar och
1.15 Uppgifter UPPGIFTER 21. Uppgift 1.1 a) Visa att transformationen x i = a ikx k med. (a ik ) =
 1.15. UPPGIFTER 1 1.15 Uppgifter Uppgift 1.1 a) isa att transformationen x i = a ikx k med (a ik ) = 1 0 1 1 1 1 1 1 1 är en rotation. b) Bestäm komponenterna T ik om (T ik ) = 0 1 0 1 0 1 0 1 0 Uppgift
1.15. UPPGIFTER 1 1.15 Uppgifter Uppgift 1.1 a) isa att transformationen x i = a ikx k med (a ik ) = 1 0 1 1 1 1 1 1 1 är en rotation. b) Bestäm komponenterna T ik om (T ik ) = 0 1 0 1 0 1 0 1 0 Uppgift
x ( f u 2y + f v 2x) xy = 24 och C = f
 Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
Institutionen för Matematik, KTH Torbjörn Kolsrud SF160, Differential- och integralkalkyl II, del 2, flervariabel, för F1. Tentamen onsdag 0 maj 2012, 8.00-1.00 Förslag till lösningar 1. Bestäm tangentplanet
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar
 FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 17, 2018 2. Kroklinjiga koordinater Allmänt behöver vi tre parametrar
FFM234, Klassisk fysik och vektorfält - Föreläsningsanteckningar Christian Forssén, Institutionen för fysik, Chalmers, Göteborg, Sverige Sep 17, 2018 2. Kroklinjiga koordinater Allmänt behöver vi tre parametrar
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A. 1. En svängningsrörelse beskrivs av
 SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
SF166 Flervariabelanalys Lösningsförslag till tentamen 13-3-1 DEL A 1. En svängningsrörelse beskrivs av ( πx ) u(x, t) = A cos λ πft där amplituden A, våglängden λ och frekvensen f är givna konstanter.
Institutionen för Matematik, KTH Torbjörn Kolsrud
 Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
Institutionen för Matematik, KTH Torbjörn Kolsrud 5B 7, ifferential- och integralkalkyl II, del 2, flervariabel, för F. Tentamen fredag 25 maj 27, 8.-3. Förslag till lösningar (ändrat 28/5-7, 29/5-7).
23 Konservativa fält i R 3 och rotation
 Nr 23, 7 maj -5, Amelia 2 23 Konservativa fält i R 3 och rotation 23. Potential 23.. Två dimensioner (2D) I två dimensioner definierade vi ett vektorfält som konservativt om kurvintegralen av fältet endast
Nr 23, 7 maj -5, Amelia 2 23 Konservativa fält i R 3 och rotation 23. Potential 23.. Två dimensioner (2D) I två dimensioner definierade vi ett vektorfält som konservativt om kurvintegralen av fältet endast
Formelsamling. Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01
 Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
Formelsamling Elektromagnetisk fältteori för F och Pi ETE055 & ETEF01 Institutionen för elektro- och informationsteknik Lunds tekniska högskola Juni 014 Innehåll 1 Elstatik 1 Likström 4 3 Magnetostatik
22 Vektoranalys och flödesintegraler
 Nr, maj -5, Amelia ektoranalys och flödesintegraler. Mera om gradient ( ), divergens ( ) och rotation ( ) Notera att ett vektorfält är en funktion R 3 R 3 (fetstil F) medan ett skalärt fält är en funktion
Nr, maj -5, Amelia ektoranalys och flödesintegraler. Mera om gradient ( ), divergens ( ) och rotation ( ) Notera att ett vektorfält är en funktion R 3 R 3 (fetstil F) medan ett skalärt fält är en funktion
Outline. TMA043 Flervariabelanalys E2 H09. Carl-Henrik Fant
 Outline TMA043 Flervariabelanalys E2 H09 Matematiska vetenskaper halmers Göteborgs universitet tel. (arb) 772 35 57 epost: carl-henrik.fant@chalmers.se Flervariabelanalys E2, Vecka 6 Ht09 Kapitel 6. -
Outline TMA043 Flervariabelanalys E2 H09 Matematiska vetenskaper halmers Göteborgs universitet tel. (arb) 772 35 57 epost: carl-henrik.fant@chalmers.se Flervariabelanalys E2, Vecka 6 Ht09 Kapitel 6. -
Flervariabelanalys E2, Vecka 6 Ht08
 Flervariabelanalys E2, Vecka 6 Ht08 Omfattning 6., 6.3-6.5 Innehåll: Gradient, divergens, rotation, Greens sats/formel, divergenssatsen i två och tre dimensioner, tokes sats tma043 V6, Ht08 bild Mål: För
Flervariabelanalys E2, Vecka 6 Ht08 Omfattning 6., 6.3-6.5 Innehåll: Gradient, divergens, rotation, Greens sats/formel, divergenssatsen i två och tre dimensioner, tokes sats tma043 V6, Ht08 bild Mål: För
A = D. r s r t dsdt. [(1 + 4t 2 ) 3/2 1]dt (1) där det sista steget fås genom variabelbytet u = 1 + 4s 2. Integralen. (1 + 4t 2 ) 3/2 dt
![A = D. r s r t dsdt. [(1 + 4t 2 ) 3/2 1]dt (1) där det sista steget fås genom variabelbytet u = 1 + 4s 2. Integralen. (1 + 4t 2 ) 3/2 dt A = D. r s r t dsdt. [(1 + 4t 2 ) 3/2 1]dt (1) där det sista steget fås genom variabelbytet u = 1 + 4s 2. Integralen. (1 + 4t 2 ) 3/2 dt](/thumbs/95/124083473.jpg) TATA44 Lösningar till tentamen 27/8/2..) Arean A av ytstycket ges av formeln A r s r t dsdt där : s t, t. En enkel räkning ger r s r t ( 2s 2 cos t, 2s 2 sin t, s) av vilket det följer att A s2 + 4s 4
TATA44 Lösningar till tentamen 27/8/2..) Arean A av ytstycket ges av formeln A r s r t dsdt där : s t, t. En enkel räkning ger r s r t ( 2s 2 cos t, 2s 2 sin t, s) av vilket det följer att A s2 + 4s 4
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF66 Flervariabelanalys Lösningsförslag till tentamen 4-3-7 EL A. Betrakta funktionen f, y y. a Beräkna riktningsderivatan av f i punkten, i den riktning som ges av vektorn 4, 3. p b Finns det någon riktning
SF66 Flervariabelanalys Lösningsförslag till tentamen 4-3-7 EL A. Betrakta funktionen f, y y. a Beräkna riktningsderivatan av f i punkten, i den riktning som ges av vektorn 4, 3. p b Finns det någon riktning
Tentamen: Lösningsförslag
 Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
Tentamen: Lösningsförslag Onsdag 5 mars 7 8:-3: SF674 Flervariabelanalys Inga hjälpmedel är tillåtna. Max: 4 poäng. 4 poäng Avgör om följande gränsvärde existerar och beräkna gränsvärdet om det existerar:
1 x. SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 26-3-2 DEL A. Låt D vara fyrhörningen med hörn i punkterna, ), 6, ),, 5) och 4, 5). a) Skissera fyrhörningen D och beräkna dess area. p) b) Bestäm
SF626 Flervariabelanalys Lösningsförslag till tentamen 26-3-2 DEL A. Låt D vara fyrhörningen med hörn i punkterna, ), 6, ),, 5) och 4, 5). a) Skissera fyrhörningen D och beräkna dess area. p) b) Bestäm
TATA44 Lösningar 24/8/ ) Låt S vara den del av x 2 + y 2 + z 2 = 2 innanför cylindern x 2 + y 2 = 1. Inför cylinderkoordinater.
 TATA Lösningar /8/.. Låt vara den del av x + y + z innanför cylindern x + y. Inför cylinderkoordinater. Parametrisera med ortsvektorn r(ρ, φ (ρ cos φ, ρ sin φ, ρ som man kan skriva som r(ρ, φ ρ ˆρ + ρ
TATA Lösningar /8/.. Låt vara den del av x + y + z innanför cylindern x + y. Inför cylinderkoordinater. Parametrisera med ortsvektorn r(ρ, φ (ρ cos φ, ρ sin φ, ρ som man kan skriva som r(ρ, φ ρ ˆρ + ρ
Inlämningsuppgift nr 2, lösningar
 UPPALA UNIVRITT MATMATIKA INTITUTIONN Bo tyf Flervariabelanalys K, X m.fl. Höstterminen 8 Inlämningsuppgift nr, lösningar. Visa att ekvationen x + x(y ) + (y ) + z + sin(yz) definierar z som en funktion
UPPALA UNIVRITT MATMATIKA INTITUTIONN Bo tyf Flervariabelanalys K, X m.fl. Höstterminen 8 Inlämningsuppgift nr, lösningar. Visa att ekvationen x + x(y ) + (y ) + z + sin(yz) definierar z som en funktion
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
SF1626 Flervariabelanalys Lösningsförslag till tentamen 215-3-16 DEL A 1. Låt f(x, y) = 1 x 2 y 2. (a) Skissa nivåkurvorna f(x, y) = c till f för c =, c = 1 och c = 2. (1 p) (b) Beräkna gradf(x, y) i de
Repetition, Matematik 2 för lärare. Ï x + 2y - 3z = 1 Ô Ì 3x - y + 2z = a Ô Á. . Beräkna ABT. Beräkna (AB) T
 Repetition, Matematik 2 för lärare Ï -2x + y + 2z = 3 1. Ange för alla reella a lösningsmängden till ekvationssystemet Ì ax + 2y + z = 1. Ó x + 3y - z = 4 2. Vad är villkoret på talet a för att ekvationssystemet
Repetition, Matematik 2 för lärare Ï -2x + y + 2z = 3 1. Ange för alla reella a lösningsmängden till ekvationssystemet Ì ax + 2y + z = 1. Ó x + 3y - z = 4 2. Vad är villkoret på talet a för att ekvationssystemet
Lösningsförslag till tentamen Torsdag augusti 16, 2018 DEL A
 Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
Institutionen för matematik SF1626 Flervariabelanalys Torsdag augusti 16, 2018 DEL A 1. Givet funktionen f(x, y) = ln(x 2 y 2 ). a) Bestäm definitionsmängden D för f. Rita även en bild av D. (2 p) b) Bestäm
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM234 och FFM232)
 Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
Lösningsskiss för tentamen Vektorfält och klassisk fysik (FFM23 och FFM232) Tid och plats: Måndagen den 29 oktober 208 klockan 00-800, Maskinsalar Lösningsskiss: Christian Forssén Detta är enbart en skiss
Flervariabelanalys E2, Vecka 5 Ht08
 Omfattning och innehåll Flervariabelanalys E2, Vecka 5 Ht08 15.1 Vektorfält och skalärfält 15.2 Konservativa vektorfält (t.o.m. exempel 5) 15.3 Kurvintegraler 15.4 Kurvintegral av vektorfält 15.5 Ytor
Omfattning och innehåll Flervariabelanalys E2, Vecka 5 Ht08 15.1 Vektorfält och skalärfält 15.2 Konservativa vektorfält (t.o.m. exempel 5) 15.3 Kurvintegraler 15.4 Kurvintegral av vektorfält 15.5 Ytor
Elektromagnetiska fält och Maxwells ekavtioner. Mats Persson
 Föreläsning 26/9 Elektromagnetiska fält och Maxwells ekavtioner 1 Maxwells ekvationer Mats Persson Maxwell satte 1864 upp fyra stycken ekvationer som gav en fullständig beskrivning av ett elektromagnetiskt
Föreläsning 26/9 Elektromagnetiska fält och Maxwells ekavtioner 1 Maxwells ekvationer Mats Persson Maxwell satte 1864 upp fyra stycken ekvationer som gav en fullständig beskrivning av ett elektromagnetiskt
AB2.1: Grundläggande begrepp av vektoranalys
 AB2.1: Grundläggande begrepp av vektoranalys En vektor är en storhet som dels har icke-negativ storlek dels har riktning i rummet. Två vektorer a och b är lika, a = b, om de har samma storlek och samma
AB2.1: Grundläggande begrepp av vektoranalys En vektor är en storhet som dels har icke-negativ storlek dels har riktning i rummet. Två vektorer a och b är lika, a = b, om de har samma storlek och samma
SF1626 Flervariabelanalys Tentamen 18 augusti 2011, Svar och lösningsförslag
 SF166 Flervariabelanalys entamen 18 augusti 11, 14. - 19. Svar och lösningsförslag 1) Låt fx, y) = xy lnx + y ). I vilken riktning är riktningsderivatan till f i punkten 1, ) som störst, och hur stor är
SF166 Flervariabelanalys entamen 18 augusti 11, 14. - 19. Svar och lösningsförslag 1) Låt fx, y) = xy lnx + y ). I vilken riktning är riktningsderivatan till f i punkten 1, ) som störst, och hur stor är
MATEMATIK GU. LLMA60 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 2014. Block 5, översikt
 MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
MATEMATIK GU H4 LLMA6 MATEMATIK FÖR LÄRARE, GYMNASIET Analys, ht 24 I block 5 ingår följande avsnitt i Stewart: Kapitel 2, utom avsnitt 2.4 och 2.6; kapitel 4. Block 5, översikt Första delen av block 5
5 Gauss sats. div. dv = A V. Noterbart är att V AdV = A ˆNdS, dvs Gauss sats, har strukturella likheter med b df
 5 Gauss sats Betrakta ett vektorfält A. i låter en sluten ta, med utåtriktad normal ˆN, begränsa ett område. Antag nu att A är kontinuerligt deriverbart i hela. Under dessa premisser gäller Gauss sats
5 Gauss sats Betrakta ett vektorfält A. i låter en sluten ta, med utåtriktad normal ˆN, begränsa ett område. Antag nu att A är kontinuerligt deriverbart i hela. Under dessa premisser gäller Gauss sats
u av funktionen u = u(x, y, z) = xyz i punkten M o = (x o, y o, z o ) = (1, 1, 1) i riktningen mot punkten M 1 = (x 1, y 1, z 1 ) = (2, 3, 1)
 ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
ATM-Matematik Mikael Forsberg 734 41 3 31 Flervariabelanalys mag31 1669 Skrivtid: 9:-14:. Inga hjälpmedel förutom bifogad formelsamling. Lösningarna skall vara fullständiga och lätta att följa. Börja varje
VIKTIGA TILLÄMPNINGAR AV GRUNDLÄGGANDE BEGREPP
 Appendix VIKTIGA TIÄMPNINGA AV GUNDÄGGANDE BEGEPP I detta appendix diskuteras viktiga tillämpningar av grundläggande begrepp inom vektoranalysen. Exemplen är främst hämtade från den elektromagnetiska teorin.
Appendix VIKTIGA TIÄMPNINGA AV GUNDÄGGANDE BEGEPP I detta appendix diskuteras viktiga tillämpningar av grundläggande begrepp inom vektoranalysen. Exemplen är främst hämtade från den elektromagnetiska teorin.
Elektromagnetiska falt och Maxwells ekavtioner
 Forelasning /1 Elektromagnetiska falt och Maxwells ekavtioner 1 Maxwells ekvationer Maxwell satte 1864 upp fyra stycken ekvationer som gav en fullstandig beskrivning av ett elektromagnetiskt falt. Dock,
Forelasning /1 Elektromagnetiska falt och Maxwells ekavtioner 1 Maxwells ekvationer Maxwell satte 1864 upp fyra stycken ekvationer som gav en fullstandig beskrivning av ett elektromagnetiskt falt. Dock,
1.Extra : Vektorer och Tensorer
 Fysiken Matematiska Metoder : Tensorer 37 1.Extra : Vektorer och Tensorer Vektorer - transformationsegenskaper Låt r vara en ortsvektor i R 3 ( 3-dimensionella rummet) och låt den representeras av två
Fysiken Matematiska Metoder : Tensorer 37 1.Extra : Vektorer och Tensorer Vektorer - transformationsegenskaper Låt r vara en ortsvektor i R 3 ( 3-dimensionella rummet) och låt den representeras av två
SF1626 Flervariabelanalys Tentamen Måndagen den 21 mars 2016
 Institutionen för matematik SF626 Flervariabelanalys Tentamen Måndagen den 2 mars 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Institutionen för matematik SF626 Flervariabelanalys Tentamen Måndagen den 2 mars 26 Skrivtid: 8:-3: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger maximalt
Poissons ekvation och potentialteori Mats Persson
 1 ärmeledning Föreläsning 21/9 Poissons ekvation och potentialteori Mats Persson i vet att värme strömmar från varmare till kallare. Det innebär att vi har ett flöde av värmeenergi i en riktning som är
1 ärmeledning Föreläsning 21/9 Poissons ekvation och potentialteori Mats Persson i vet att värme strömmar från varmare till kallare. Det innebär att vi har ett flöde av värmeenergi i en riktning som är
SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 2015
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 215 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Måndagen den 16 mars 215 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
* Läsvecka 1 * Läsvecka 2 * Läsvecka 3 * Läsvecka 4 * Läsvecka 5 * Läsvecka 6 * Läsvecka 7 * Tentamenssvecka. Läsvecka 1
 Detta är en preliminär planering över undervisningen i kursen och är tänkt att hjälpa dig att få ut så mycket som möjligt av föreläsningarna. Till varje föreläsningsdag finns förberedelser, innehåll och
Detta är en preliminär planering över undervisningen i kursen och är tänkt att hjälpa dig att få ut så mycket som möjligt av föreläsningarna. Till varje föreläsningsdag finns förberedelser, innehåll och
Matematikuppgifter del II, FYTA11
 Matematikuppgifter del II, FYTA11 51. Lös uppgift 10.1 i boken. 52. Lös uppgift 10.2 i boken. 53. Lös uppgift 10.3 i boken. 54. Lös uppgift 10.4 i boken. 55. Låt en kurva i rummet vara given i parametrisk
Matematikuppgifter del II, FYTA11 51. Lös uppgift 10.1 i boken. 52. Lös uppgift 10.2 i boken. 53. Lös uppgift 10.3 i boken. 54. Lös uppgift 10.4 i boken. 55. Låt en kurva i rummet vara given i parametrisk
Karta över Jorden - viktigt exempel. Sfär i (x, y, z) koordinater Funktionen som beskriver detta ser ut till att vara
 Föreläsning 1 Jag hettar Thomas Kragh och detta är kursen: Flervariabelanalys 1MA016/1MA183. E-post: thomas.kragh@math.uu.se Kursplan finns i studentportalens hemsida för denna kurs. Där är två spår: Spår
Föreläsning 1 Jag hettar Thomas Kragh och detta är kursen: Flervariabelanalys 1MA016/1MA183. E-post: thomas.kragh@math.uu.se Kursplan finns i studentportalens hemsida för denna kurs. Där är två spår: Spår
FFM232, Klassisk fysik och vektorfält - Veckans tal
 FFM232, Klassisk fysik och vektorfält - eckans tal Tobias Wenger och Christian Forssén, Chalmers, Göteborg, Sverige Oct 3, 2016 Uppgift 6.6 (Cederwalls kompendium) Beräkna normalytintegralen av a F 2 [
FFM232, Klassisk fysik och vektorfält - eckans tal Tobias Wenger och Christian Forssén, Chalmers, Göteborg, Sverige Oct 3, 2016 Uppgift 6.6 (Cederwalls kompendium) Beräkna normalytintegralen av a F 2 [
AB2.5: Ytor och ytintegraler. Gauss divergenssats
 AB2.5: Ytor och ytintegraler. Gauss divergenssats Ytor på parameterform Låt xyz vara ett cartesiskt koordinatsystem i rummet. En yta på parameterform ges av tre ekvationer x = x(u, v), y = y(u, v), z =
AB2.5: Ytor och ytintegraler. Gauss divergenssats Ytor på parameterform Låt xyz vara ett cartesiskt koordinatsystem i rummet. En yta på parameterform ges av tre ekvationer x = x(u, v), y = y(u, v), z =
Tentamen i Flervariabelanalys, MVE , π, kl
 Tentamen i Flervariabelanalys, MVE35 216-3-14, π, kl. 14.-18. Hjälpmedel: Inga, ej räknedosa. Telefon: anknytning 5325 Telefonvakt: Raad Salman För godkänt krävs minst 2 poäng. Betyg 3: 2-29 poäng, betyg
Tentamen i Flervariabelanalys, MVE35 216-3-14, π, kl. 14.-18. Hjälpmedel: Inga, ej räknedosa. Telefon: anknytning 5325 Telefonvakt: Raad Salman För godkänt krävs minst 2 poäng. Betyg 3: 2-29 poäng, betyg
y= x dx = x = r cosv $ y = r sin v ,dxdy = rdrdv ' 2* så får vi att
 TH-Matematik Lösningsförslag till Tentamenskrivning 5-6-, kl. 8.-3. 5B7, matematik III för E och ME 6p) Del A, 3-poängsuppgifter x. xy y )dy dx x y y3 3 ) * x 3 x3 3, x3 -. dx 5 5 x4 6 4 y x y 5 4 dx.
TH-Matematik Lösningsförslag till Tentamenskrivning 5-6-, kl. 8.-3. 5B7, matematik III för E och ME 6p) Del A, 3-poängsuppgifter x. xy y )dy dx x y y3 3 ) * x 3 x3 3, x3 -. dx 5 5 x4 6 4 y x y 5 4 dx.
October 9, Innehållsregister
 October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
October 9, 017 Innehållsregister 1 Vektorer 1 1.1 Geometrisk vektor............................... 1 1. Vektor och koordinatsystem.......................... 1 1.3 Skalär produkt (dot eller inner product)...................
4 Integrering av vektorfält
 4 Integrering av vektorfält 4.1 Integrering av vektorvärda funktioner Vi börjar vår undersökning av hur vektorfält integreras med att studera en styckvis kontinuerlig funktion A av flera oberoende variabler
4 Integrering av vektorfält 4.1 Integrering av vektorvärda funktioner Vi börjar vår undersökning av hur vektorfält integreras med att studera en styckvis kontinuerlig funktion A av flera oberoende variabler
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
SF1626 Flervariabelanalys Lösningsförslag till tentamen 216-6-7 DEL A 1. Låt S vara ellipsoiden som ges av ekvationen x 2 + 2y 2 + 3z 2 = 5. (a) Bestäm en normalvektor till S i en punkt (x, y, z ) på S.
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF66 Flervariabelanals Lösningsförslag till tentamen --9 EL A. En kulle beskrivs approximativt av funktionen 5 hx, ) + 3x + i lämpliga enheter där hx, ) är höjden. Om du befinner dig i punkten,, ) på kullen,
SF66 Flervariabelanals Lösningsförslag till tentamen --9 EL A. En kulle beskrivs approximativt av funktionen 5 hx, ) + 3x + i lämpliga enheter där hx, ) är höjden. Om du befinner dig i punkten,, ) på kullen,
14. Potentialer och fält
 4. Potentialer och fält [Griffiths,RMC] För att beräkna strålningen från kontinuerliga laddningsfördelningar och punktladdningar måste deras el- och magnetfält vara kända. Dessa är i de flesta fall enklast
4. Potentialer och fält [Griffiths,RMC] För att beräkna strålningen från kontinuerliga laddningsfördelningar och punktladdningar måste deras el- och magnetfält vara kända. Dessa är i de flesta fall enklast
SF1669 Matematisk och numerisk analys II Bedömningskriterier till tentamen Måndagen den 16 mars 2015
 SF1669 Matematisk och numerisk analys II Bedömningskriterier till tentamen Måndagen den 16 mars 2015 Allmänt gäller följande: För full poäng på en uppgift krävs att lösningen är väl presenterad och lätt
SF1669 Matematisk och numerisk analys II Bedömningskriterier till tentamen Måndagen den 16 mars 2015 Allmänt gäller följande: För full poäng på en uppgift krävs att lösningen är väl presenterad och lätt
1. För vilka värden på konstanterna a och b är de tre vektorerna (a,b,b), (b,a,b) och (b,b,a) linjärt beroende.
 Institutionen för matematik KTH MOELLTENTAMEN Tentamensskrivning, år månad dag, kl. x. (x + 5).. 5B33, Analytiska metoder och linjär algebra. Uppgifterna 5 svarar mot varsitt moment i den kontinuerliga
Institutionen för matematik KTH MOELLTENTAMEN Tentamensskrivning, år månad dag, kl. x. (x + 5).. 5B33, Analytiska metoder och linjär algebra. Uppgifterna 5 svarar mot varsitt moment i den kontinuerliga
TMV036 Analys och Linjär Algebra K Kf Bt, del C
 MATEMATIK Hjälpmedel: Inga Chalmers tekniska högskola Datum: -- kl 4 8 Tentamen Telefonvakt: Richard Lärkäng tel 3-8834 TMV36 Analys och Linjär Algebra K Kf Bt, del C Tentan rättas och bedöms anonymt Skriv
MATEMATIK Hjälpmedel: Inga Chalmers tekniska högskola Datum: -- kl 4 8 Tentamen Telefonvakt: Richard Lärkäng tel 3-8834 TMV36 Analys och Linjär Algebra K Kf Bt, del C Tentan rättas och bedöms anonymt Skriv
Övning 6, FMM-Vektoranalys, SI1140
 Övning 6, FMM-ektoranalys, I114 ˆ 6. Beräkna integralen där A dr A x 2 ay + z) ) e x + y 2 az ) e y + z 2 ax + y) ) e z och är den kurva som utgör skärningslinjen mellan cylindern { x a) 2 + y 2 a 2 och
Övning 6, FMM-ektoranalys, I114 ˆ 6. Beräkna integralen där A dr A x 2 ay + z) ) e x + y 2 az ) e y + z 2 ax + y) ) e z och är den kurva som utgör skärningslinjen mellan cylindern { x a) 2 + y 2 a 2 och
Vektorgeometri. En vektor v kan representeras genom pilar från en fotpunkt A till en spets B.
 Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
Vektorgeometri En vektor v kan representeras genom pilar från en fotpunkt A till en spets B. Två pilar AB, A B tilllhör samma vektor om de har samma riktning och samma längd. Vi skriver v = AB = B A B
SF1626 Flervariabelanalys
 1 / 28 SF1626 Flervariabelanalys Föreläsning 2 Hans Thunberg Institutionen för matematik, KTH VT 2018, Period 4 2 / 28 SF1626 Flervariabelanalys Dagens lektion: avsnitt 11.1 11.3 Funktioner från R till
1 / 28 SF1626 Flervariabelanalys Föreläsning 2 Hans Thunberg Institutionen för matematik, KTH VT 2018, Period 4 2 / 28 SF1626 Flervariabelanalys Dagens lektion: avsnitt 11.1 11.3 Funktioner från R till
Linjära avbildningar. Låt R n vara mängden av alla vektorer med n komponenter, d.v.s. x 1 x 2. x = R n = x n
 Linjära avbildningar Låt R n vara mängden av alla vektorer med n komponenter, d.v.s. R n = { x = x x. x n } x, x,..., x n R. Vi räknar med vektorer x, y likandant som i planet och i rymden. vektorsumma:
Linjära avbildningar Låt R n vara mängden av alla vektorer med n komponenter, d.v.s. R n = { x = x x. x n } x, x,..., x n R. Vi räknar med vektorer x, y likandant som i planet och i rymden. vektorsumma:
SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen DEL A. r cos t + (r cos t) 2 + (r sin t) 2) rdrdt.
 1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
1. Beräkna integralen medelpunkt i origo. SF1669 Matematisk och numerisk analys II Lösningsförslag till tentamen 218-3-14 D DEL A (x + x 2 + y 2 ) dx dy där D är en cirkelskiva med radie a och Lösningsförslag.
Repetition kapitel 21
 Repetition kapitel 21 Coulombs lag. Grundbulten! Definition av elektriskt fält. Fält från punktladdning När fältet är bestämt erhålls kraften ur : F qe Definition av elektrisk dipol. Moment och energi
Repetition kapitel 21 Coulombs lag. Grundbulten! Definition av elektriskt fält. Fält från punktladdning När fältet är bestämt erhålls kraften ur : F qe Definition av elektrisk dipol. Moment och energi
Lösningsförslag till tentamen Onsdagen den 15 mars 2017 DEL A
 Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Onsdagen den 5 mars 7 DEL A. I nedanstående rätvinkliga koordinatsystem är varje ruta en enhet lång. (a) Bestäm de rymdpolära
Institutionen för matematik SF66 Flervariabelanalys Lösningsförslag till tentamen Onsdagen den 5 mars 7 DEL A. I nedanstående rätvinkliga koordinatsystem är varje ruta en enhet lång. (a) Bestäm de rymdpolära
SF1646 Analys i flera variabler Tentamen 18 augusti 2011, Svar och lösningsförslag
 SF1646 Analys i flera variabler Tentamen 18 augusti 11, 14. - 19. Svar och lösningsförslag (1) Låt f(x, y) = xy ln(x + y ). I vilken riktning är riktningsderivatan till f i punkten (1, ) som störst, och
SF1646 Analys i flera variabler Tentamen 18 augusti 11, 14. - 19. Svar och lösningsförslag (1) Låt f(x, y) = xy ln(x + y ). I vilken riktning är riktningsderivatan till f i punkten (1, ) som störst, och
Analys o Linjär algebra. Lektion 7.. p.1/65
 Analys o Lektion 7 p1/65 Har redan (i matlab bla) stött på tal-listor eller vektorer av typen etc Vad kan sådana tänkas representera/modellera? Hur kan man räkna med sådana? Skall närmast fokusera på ordnade
Analys o Lektion 7 p1/65 Har redan (i matlab bla) stött på tal-listor eller vektorer av typen etc Vad kan sådana tänkas representera/modellera? Hur kan man räkna med sådana? Skall närmast fokusera på ordnade
SF1626 Flervariabelanalys Lösningsförslag till tentamen DEL A
 SF626 Flervariabelanalys Lösningsförslag till tentamen 23-- DEL A. Bestäm en ekvation för tangentplanet i punkten (,, 2 till ellipsoiden 2x 2 +3y 2 +z 2 = 9. (4 p Lösning. Vi uppfattar ytan som nivåytan
SF626 Flervariabelanalys Lösningsförslag till tentamen 23-- DEL A. Bestäm en ekvation för tangentplanet i punkten (,, 2 till ellipsoiden 2x 2 +3y 2 +z 2 = 9. (4 p Lösning. Vi uppfattar ytan som nivåytan
SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 2016
 Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Institutionen för matematik SF1626 Flervariabelanalys Tentamen Tisdagen den 7 juni 216 Skrivtid: 8:-13: Tillåtna hjälpmedel: inga Examinator: Mats Boij Tentamen består av nio uppgifter som vardera ger
Tentamen Modellering och simulering inom fältteori, 21 oktober, 2006
 Institutionen för elektrovetenskap Tentamen Modellering och simulering inom fältteori, oktober, 006 Tillåtna hjälpmedel: Formelsamling i Elektromagnetisk fältteori Varje uppgift ger 0 poäng. Delbetyget
Institutionen för elektrovetenskap Tentamen Modellering och simulering inom fältteori, oktober, 006 Tillåtna hjälpmedel: Formelsamling i Elektromagnetisk fältteori Varje uppgift ger 0 poäng. Delbetyget
21 Flödesintegraler och Gauss sats
 Nr 2, maj -5, Amelia 2 2 Flödesintegraler och Gauss sats 2. DivergensochGausssats 2.. Flöden genom slutna ytor I detta avsnitt beräknar vi flödesintgraler på slutna ytor. Låt oss tänka oss en vind, som
Nr 2, maj -5, Amelia 2 2 Flödesintegraler och Gauss sats 2. DivergensochGausssats 2.. Flöden genom slutna ytor I detta avsnitt beräknar vi flödesintgraler på slutna ytor. Låt oss tänka oss en vind, som
1 Ortogonalitet. 1.1 Skalär produkt. Man kan tala om vinkel mellan vektorer.
 Ortogonalitet Man kan tala om vinkel mellan vektorer.. Skalär produkt Vi definierar längden (eller normen) av en vektor som ett reellt tal 0 (Se boken avsnitt.). Vi definierar skalär produkt (Inner product),
Ortogonalitet Man kan tala om vinkel mellan vektorer.. Skalär produkt Vi definierar längden (eller normen) av en vektor som ett reellt tal 0 (Se boken avsnitt.). Vi definierar skalär produkt (Inner product),
